Completeness of the real numbers
Intuitively, completeness implies that there are not any “gaps” (in Dedekind's terminology) or “missing points” in the real number line. This contrasts with the rational numbers, whose corresponding number line has a “gap” at each irrational value. In the decimal number system, completeness is equivalent to the statement that any infinite string of decimal digits is actually the decimal representation for some real number.
Depending on the construction of the real numbers used completeness may take the form of an axiom (the completeness axiom), or may be a theorem proven from the construction. There are many equivalent forms of completeness, the most prominent being Dedekind completeness (the least-upper-bound property) and Cauchy completeness (completeness as a metric space).
Contents |
Forms of completeness
The real numbers can be defined synthetically as an ordered field satisfying some version of the completeness axiom. Different versions of this axiom are all equivalent, in the sense that any ordered field that satisfies one form of completeness satisfies all of them. When the real numbers are instead constructed using a model, completeness becomes a theorem or collection of theorems.
Dedekind completeness
Dedekind completeness, also known as the least-upper-bound property, states that every nonempty set of real numbers having an upper bound must have a least upper bound (or supremum). In a synthetic approach to the real numbers, this is the version of completeness that is most often stated as an axiom.
The rational number line Q is not Dedekind complete. An example is the subset of rational numbers
The number 5 is certainly an upper bound for the set. However, this set has no least upper bound in Q: the least upper bound in this case is 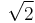 which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.
which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.
Dedekind completeness is related to the construction of the real numbers using Dedekind cuts. Essentially, this method defines a real number to be the least upper bound of some set of rational numbers.
In the order of the theory x Dedekind completeness can be generalized to any partially ordered set. See completeness (order theory).
Cauchy completeness
Cauchy completeness is the statement that every Cauchy sequence of real numbers converges.
The rational number line Q is not Cauchy complete. An example is the following sequence of rational numbers:
Here the nth term in the sequence is the nth decimal approximation for pi. Though this is a Cauchy sequence of rational numbers, it does not converge to any rational number. (In this real number line, this sequence converges to pi.)
Cauchy completeness is related to the construction of the real numbers using Cauchy sequences. Essentially, this method defines a real number to be the limit of a Cauchy sequence of rational numbers.
In mathematical analysis, Cauchy completeness can be generalized to a notion of completeness for any metric space. See complete metric space.
Nested intervals theorem
The nested interval theorem is another form of completeness. Let In = [an, bn] be a sequence of closed intervals, and suppose that these intervals are nested in the sense that
- I1 ⊇ I2 ⊇ I3 ⊇ ⋯.
The nested interval theorem states that the intersection of all of the intervals In is nonempty.
The rational number line does not satisfy the nested interval theorem. For example, the sequence
is a nested sequence of closed intervals in the rational numbers whose intersection is empty. (In the real numbers, the intersection of these intervals contains the number pi.)
Monotone convergence theorem
The monotone convergence theorem (described as the fundamental axiom of analysis by Körner (2004)) states that every nondecreasing, bounded sequence of real numbers converges. This can be viewed as a special case of Dedekind completeness, but it can also be used fairly directly to prove the Cauchy completeness of the real numbers.
Bolzano–Weierstrass theorem
The Bolzano–Weierstrass theorem states that every bounded sequence of real numbers has a convergent subsequence. Again, this theorem is equivalent to the other forms of completeness given above.
See also
References
- Aliprantis, Charalambos D; Burkinshaw, Owen (1998). Principles of real analysis (Third ed.). Academic. ISBN 0-12-050257-7.
- Browder, Andrew (1996). Mathematical Analysis: An Introduction. Undergraduate Texts in Mathematics. New York: Springer-Verlag. ISBN 0-387-94614-4.
- Bartle, Robert G. and Sherbert, Donald R. (2000). Introduction to Real Analysis (3 ed.). New York: John Wiley and Sons. ISBN 0-471-32148-6.
- Abbott, Stephen (2001). Understanding Analysis. Undergradutate Texts in Mathematics. New York: Springer-Verlag. ISBN 0-387-95060-5.
- Körner, Thomas William (2004), A companion to analysis: a second first and first second course in analysis, AMS Chelsea, ISBN 9780821834473
- Rudin, Walter. Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (3 ed.). McGraw-Hill. ISBN 978-0070542358.
- Dangello, Frank and Seyfried, Michael (1999). Introductory Real Analysis. Brooks Cole. ISBN 978-0395959336.
- Bressoud, David (2007). A Radical Approach to Real Analysis. MAA. ISBN 0-883857472.
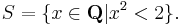
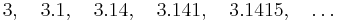
![[3,4] \;\supseteq\; [3.1,3.2] \;\supseteq\; [3.14,3.15] \;\supseteq\; [3.141,3.142] \;\supseteq\; \cdots](/2012-wikipedia_en_all_nopic_01_2012/I/fba3cbc65d9d4f79afbaf60793d444bb.png)